A kakuro solver

The kakuro puzzle

The Kakuro puzzle is a kind of logic puzzle that is often referred to as a mathematical transliteration of the crossword. It resembles Sudoku which is nowadays more popular. Kakuro puzzles can be found in newspapers (e. g. Dagens Nyheter and Svenska Dagbladet in Sweden) as well as in hobby magazines. Kakuro puzzles are hard to solve for the the beginner but becomes easier with training.

A Kakuro puzzle consists of a rectangular grid of empty cells which are to be filled with integers in the interval [1, 9]. Other cells contain row and/or column conditions. A row condition gives the sum which the empty cells to the right of it must add up to, and a column condition shows the required sum of the empty cells immediately below. Duplicates are not allowed in these sums.
A small example:

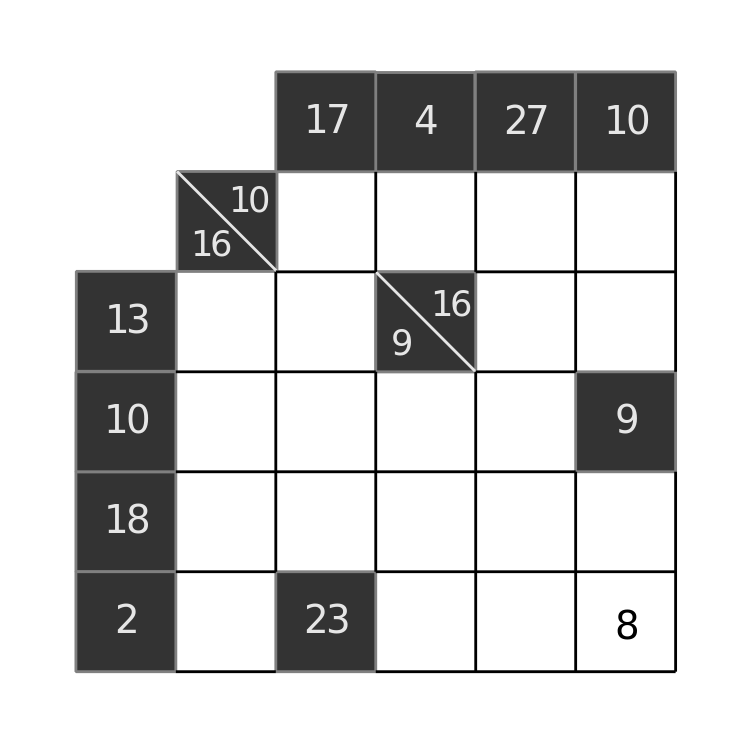
We number the rows from 0 to 5, and the columns also from 0 to 5. The contents of the empty cells of row 1 we call c₁₂,...,c₁₅. Row 1 has the associated condition that the sum of its four cell values should equal 10. Row 2 has two conditions:

13 = c₂₂ + c₂₃ and 16 = c₂₄ + c₂₅

Column 2 carries two conditions, the first of which is 4 = c₁₂. And so on. The value of c₅₅ is given explicitly as 8.

It would seem that the puzzle is defined by a system of linear equations. However added requirements of every c_ij being in the range 1..9, and that every term in a sum being different, makes it necessary to look for another approach:
Locate a row or column condition which can be satisfied in a minimum number of alternative ways! Cross your fingers and choose one of these. Then continue in the same way. In general back-tracking is necessary, of course. (The general kakuro puzzle problem has been shown to be NP-complete, that is, inherently difficult.)

The example problem above is rather easily solved by hand. Hint: the sum 23 on the last row can only be obtained in two ways. Looking at the associated column conditions one of them can be eliminated. Our example has two solutions. As a rule, published kakuro puzzles have a unique solution.

There exist variations of Kakuro. One popular form has the added condition that some cells are grey instead of white. The grey cells are to be filled with odd numbers and the white ones with even numbers. We call these puzzles "parity kakuro" puzzles. Solving kakuro puzzles by hand is is an interesting pastime. Writing a computer program solving any puzzle is still more intriguing. Working on the problem I learnt a programming language new to me: Python

The program

The idea of the program is to follow the approach outlined above, using the computer to keep track of all choices, allowing correct backtracing if a choice turns out to lead to a dead end - not an easy task. Puzzles of size 10 x 10 can be difficult for a human but are solved in a fraction of a second by the computer. (Note. The program can in rare cases make a suboptimal choice. Example: Dividing 9 into two parts can be done in 8 ways, and dividing 23 into three parts can be done in 6 ways. The program always chooses a condition among those with a minimum of empty cells. This does not mean that the program is erroneous.)

Input to the program is a text file where the row and column conditions are enumerated as well as the given cells. For the example, the text file looks as follows (r indicating a row condition, c a column condition, and b a board position):

   r1 10 2:5           (i e, 10 = c12+c13+c14+c15)
   r2 13 1:2
   r2 16 4:5
   r3 10 1:4
   r4 18 1:5
   r5  2 1
   r5 23 3:5
   c1 16 2:5           (i e, 16 = c21+c31+c41+c51)
   c2 17 1:4
   c3  4 1
   c3  9 3:5
   c4 27 1:5
   c5 10 1:2
   c5  9 4:5
   b 5 5 8             ( i e, c55 = 8) 
   .

A convenient graphical user interface is not implemented: my interest was to develop a correct solver.

Given this input file the program computes and prints the solution(s). The program library published here as a "7zip" file contains three versions, one for the standard kakuro, one verbose version for standard kakuro, and one for parity kakuro. The verbose version produces a trace showing what is going on during the computation. This trace can be long!

In case of a parity kakuro the input must enumerate the even cells - those not enumerated are considered to be odd. This is done by adding one or more lines beginning with an 'e'. For example, a 2 by 2 checkerboard where c₁₂ and c₂₁ should be odd would require the added line:

   e 11 22

Running the program

The program has been tested on Windows and Linux using the examples provided with kaklib. We assume that Python version 3 has been installed, and that kaklib.7z has been downloaded and unpacked into the folder kaklib.

On Windows:

Start Python, preferably using IDLE (the Python GUI).
Run the command from os import * to get access to the functions getcwd, chdir, listdir to move to the kaklib folder and list its files.
(Example: chdir('C:\\Users\le\Documents\kaklib'))
Run the command
from kaksolve import kaksolve
(or from kaksolvev import kaksolve for the verbose version, or from kaksolvep import kaksolve for running a parity problem)
To run one of the provided examples, say mini0.txt, run
kaksolve("Ex\mini0.txt")
For the verbose version three levels (0, 1, 2) of output information are available. The desired level is indicated by an additional argument. Example: kaksolve("Ex\mini0.txt", 2) will provide most information.
A 9 x 9 problem may generate thousands of lines of output. The program will stop producing trace after 1000 lines.
To make an example of your own, use any text editor for the input file. To inspect and/or change in the program (the .py files), use the IDLE editor (locate the file using Explorer, right-click) and choose IDLE).

On Linux:

Start a terminal window and move to the kaklib directory. Start python3. For running an example follow points 3 and 4 above. The text editors gedit and kate (for example) are helpful for editing .py files.

Any feedback would be most welcome!

5 Sep 2013
Lars-Erik Thorelli